NumPy linspace(): jak tworzyć tablice równomiernie rozmieszczonych liczb
Opublikowany: 2022-04-11Ten samouczek nauczy Cię, jak używać NumPy linspace() do tworzenia tablicy równomiernie rozmieszczonych liczb w Pythonie.
Poznasz składnię NumPy linspace() , a następnie przykłady, które pomogą Ci zrozumieć, jak z niego korzystać.
Uwaga: Aby śledzić ten samouczek, musisz mieć zainstalowany Python i NumPy.
Nie masz jeszcze NumPy? Przygotowaliśmy dla Ciebie krótki przewodnik po instalacji.
Zaczynajmy!
Zainstaluj i zaimportuj NumPy
Przed rozpoczęciem samouczka szybko prześledźmy kroki instalacji biblioteki NumPy.
Jeśli masz już zainstalowany NumPy, możesz przejść do następnej sekcji.
- Jeśli używasz Google Colab — opartego na chmurze środowiska notatników Jupyter, możesz zaimportować NumPy i od razu zacząć kodować. (zalecane w tym samouczku)
- Jeśli chcesz skonfigurować lokalne środowisko pracy, polecam zainstalowanie dystrybucji Pythona Anaconda. Anaconda zawiera kilka preinstalowanych przydatnych pakietów. Możesz pobrać instalator dla swojego systemu operacyjnego. Proces konfiguracji zajmuje tylko kilka minut.
- Jeśli masz już zainstalowany Python na swoim komputerze, nadal możesz zainstalować dystrybucję Anaconda. Możesz użyć conda lub pip do instalacji i zarządzania pakietami. Możesz uruchomić jedno z następujących poleceń z wiersza polecenia Anaconda, aby zainstalować NumPy.
# Install NumPy using conda conda install numpy # Install NumPy using pip pip install numpy W następnym kroku zaimportuj numpy pod aliasem np , uruchamiając następujące polecenie. Pomoże ci to odnieść się do NumPy jako np — bez konieczności wpisywania numpy każdym razem, gdy uzyskujesz dostęp do elementu w module.
import numpy as np Idąc dalej, użyjemy notacji z kropką, aby uzyskać dostęp do wszystkich funkcji w bibliotece NumPy w następujący sposób: np.<func-name> .
Sprawa dla równomiernie rozmieszczonych liczb
Podczas pracy z tablicami NumPy zdarza się, że trzeba utworzyć tablicę liczb równomiernie rozmieszczonych w interwale.
Zanim przejdziemy dalej, szybko przejrzyjmy inną podobną funkcję np.arange() .
NumPy linspace() kontra NumPy arange()
Jeśli używałeś wcześniej NumPy, prawdopodobnie np.arange() do utworzenia tablicy liczb w określonym zakresie.
Wiesz, że
np.arange(start, stop, step)zwraca tablicę liczb odstartdo, ale nie włączającstop, w krokachstep; domyślny rozmiar kroku to 1.
Jednak wartość kroku nie zawsze jest oczywista. Zobaczmy, dlaczego tak jest.
Na przykład, jeśli potrzebujesz 4 równomiernie rozmieszczonych liczb od 0 do 1, wiesz, że rozmiar kroku musi wynosić 0,25. Ale jeśli używasz np.arange() , nie zawiera on wartości zatrzymania równej 1. Więc będziesz musiał wybrać interwał, który wykracza poza wartość zatrzymania.
Poniższy rysunek ilustruje jeszcze kilka przykładów, w których potrzebna jest określona liczba równomiernie rozmieszczonych punktów w przedziale [a, b].
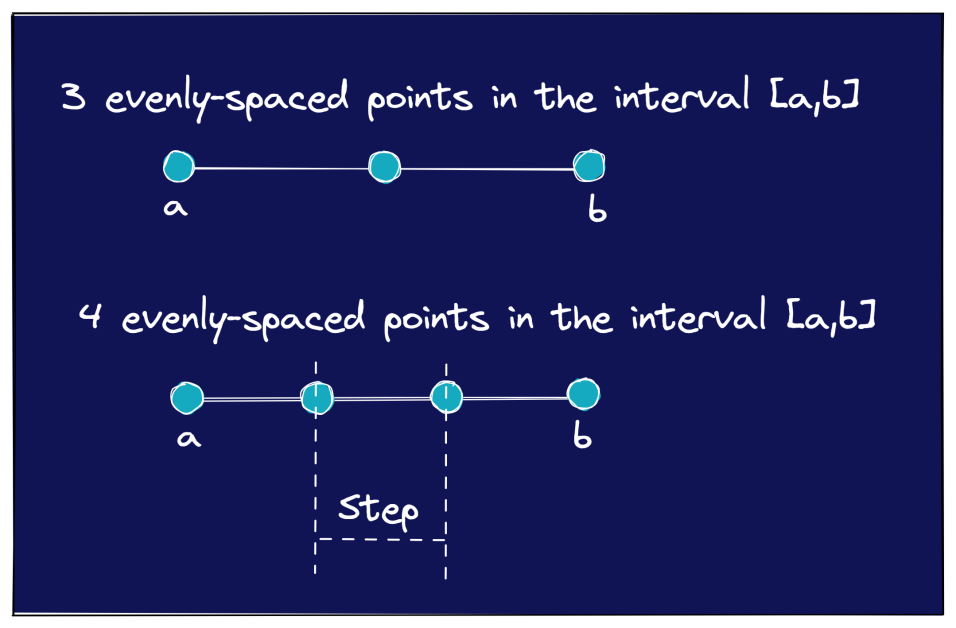
Nasz pierwszy przykład 4 równo rozmieszczonych punktów w [0,1] był dość łatwy. Wiesz, że wielkość kroku między punktami powinna wynosić 0,25.
Załóżmy, że masz nieco bardziej skomplikowany przykład — w którym musiałeś wymienić 7 równomiernie rozmieszczonych punktów od 1 do 33. W tym przypadku rozmiar kroku może nie być od razu jasny. Możesz jednak ręcznie obliczyć wartość step w tym przypadku.
Jednak np.linspace() jest tutaj, aby jeszcze bardziej to ułatwić!

Używając np.linspace() , wystarczy określić liczbę punktów w przedziale — bez martwienia się o rozmiar kroku. I otrzymasz z powrotem tablicę zgodnie z życzeniem.
Mając tę motywację, przejdźmy do nauki składni NumPy linspace() w następnej sekcji.
Składnia NumPy linspace()
Składnia używania NumPy linspace() jest pokazana poniżej:
np.linspace(start, stop, num, endpoint, retstep, dtype, axis)Na początku powyższa składnia może wydawać się bardzo skomplikowana z wieloma parametrami.
Jednak większość z nich to parametry opcjonalne , a znacznie prostszą składnię uzyskamy w ciągu zaledwie kilku minut.
Teraz zacznijmy od przeanalizowania powyższej składni:
-
starti koniec to odpowiedniostopi koniec interwału. Zarówno start, jak i stop mogą być skalarami lub tablicami. W tym samouczku ograniczymy się do skalarnych wartości początkowych i końcowych. -
numto liczba równomiernie rozmieszczonych punktów. Jest to parametr opcjonalny o domyślnej wartości 50. -
endpointjest również opcjonalnym parametrem, który może mieć wartość Prawda lub Fałsz. - Wartość domyślna to True, co oznacza, że punkt końcowy będzie domyślnie uwzględniony w przedziale. Możesz jednak ustawić go na False, aby wykluczyć punkt końcowy.
-
retstepto kolejny opcjonalny parametr, który przyjmuje wartości logiczne True lub False. Po ustawieniu na True zwracana jest wartość kroku. -
dtypeto typ danych liczb w tablicy. Typ jest zwykle wywnioskowany jako float i nie musi być podawany jawnie. -
axisto kolejny opcjonalny parametr oznaczający oś, wzdłuż której powinny być przechowywane liczby. I ma to znaczenie tylko wtedy, gdy wartościstartistopsame w sobie są tablicami.
️ Więc co np.linspace() ?
Zwraca N-wymiarową tablicę równomiernie rozmieszczonych liczb. A jeśli parametr retstep jest ustawiony na True , zwraca również rozmiar kroku.
W oparciu o dotychczasową dyskusję, oto uproszczona składnia do użycia np.linspace() :
np.linspace(start, stop, num)Powyższy wiersz kodu zwróci tablicę
numrównomiernie rozmieszczonych w przedziale[start, stop].
Teraz, gdy znasz składnię, zacznijmy kodować przykłady.
Jak tworzyć równomiernie rozmieszczone tablice za pomocą NumPy linspace()
#1. Jako nasz pierwszy przykład, utwórzmy tablicę 20 równomiernie rozmieszczonych liczb w przedziale [1, 5].

Jako argumenty słów kluczowych można określić wartości start , stop i num . Jest to pokazane w komórce kodu poniżej:
import numpy as np arr1 = np.linspace(start = 1,stop = 5,num = 20) print(arr1) # Output: [1. 1.21052632 1.42105263 1.63157895 1.84210526 2.05263158 2.26315789 2.47368421 2.68421053 2.89473684 3.10526316 3.31578947 3.52631579 3.73684211 3.94736842 4.15789474 4.36842105 4.57894737 4.78947368 5. ] Zwróć uwagę, że liczby w tablicy zaczynają się od 1 i kończą na 5 — łącznie z obydwoma punktami końcowymi. Zwróć także uwagę, jak liczby, w tym punkty 1 i 5, są reprezentowane w zwracanej tablicy jako liczby float .
#2. W poprzednim przykładzie przekazano wartości start , stop i num jako argumenty słów kluczowych . Jeśli przekażesz argumenty we właściwej kolejności, możesz równie dobrze użyć ich jako argumentów pozycyjnych z samymi wartościami, jak pokazano poniżej.
import numpy as np arr2 = np.linspace(1,5,20) print(arr2) # Output: [1. 1.21052632 1.42105263 1.63157895 1.84210526 2.05263158 2.26315789 2.47368421 2.68421053 2.89473684 3.10526316 3.31578947 3.52631579 3.73684211 3.94736842 4.15789474 4.36842105 4.57894737 4.78947368 5. ] #3. Teraz stwórzmy kolejną tablicę, w której ustawimy retstep na True .
Oznacza to, że funkcja zwróci teraz zarówno tablicę, jak i krok. I możemy rozpakować je do dwóch zmiennych arr3 : tablicy i step_size : zwróconego rozmiaru kroku.
Poniższa komórka kodu wyjaśnia, jak to zrobić.
import numpy as np arr3, step_size = np.linspace(1,5,20,retstep = True) print(arr3) # Output: [1. 1.21052632 1.42105263 1.63157895 1.84210526 2.05263158 2.26315789 2.47368421 2.68421053 2.89473684 3.10526316 3.31578947 3.52631579 3.73684211 3.94736842 4.15789474 4.36842105 4.57894737 4.78947368 5. ] # Output: print(step_size) 0.21052631578947367 #4. Jako ostatni przykład ustawmy endpoint na False i sprawdźmy, co się stanie.
import numpy as np arr4 = np.linspace(1,5,20,endpoint = False) print(arr4) # Output: [1. 1.2 1.4 1.6 1.8 2. 2.2 2.4 2.6 2.8 3. 3.2 3.4 3.6 3.8 4. 4.2 4.4 4.6 4.8]W zwróconej tablicy widać, że 1 jest uwzględnione, podczas gdy 5 nie jest uwzględnione. A ostatnia wartość w tablicy to 4,8, ale wciąż mamy 20 liczb.
Do tej pory wygenerowaliśmy tylko tablice równomiernie rozmieszczonych liczb. W następnej sekcji zwizualizujmy, wykreślając te liczby.
Jak wykreślić liczby równomiernie rozmieszczone w interwale?
W tej sekcji wybierzmy [10,15] jako interwał zainteresowania. Następnie użyj np.linspace() , aby wygenerować dwie tablice, każda z odpowiednio 8 i 12 punktami.
Po zakończeniu możemy użyć funkcji kreślenia z biblioteki matplotlib , aby je wykreślić.
Dla jasności połączymy dwie tablice N1 = 8 i N2 = 12 równomiernie rozmieszczonych punktów w różnych pozycjach wzdłuż osi y.
Poniższy fragment kodu demonstruje to.
import numpy as np import matplotlib.pyplot as plt N1 = 8 N2 = 12 a = 10 b = 15 y1 = np.zeros(N1) y2 = np.zeros(N2) x1 = np.linspace(a, b, N1) x2 = np.linspace(a, b, N2) plt.plot(x1, y1-0.5, 'o') plt.plot(x2, y2 + 0.5, 'o') plt.ylim([-1, 1]) plt.title(f'Evenly Spaced Numbers in the Interval [{a},{b}]') plt.xlabel('Interval') plt.show() 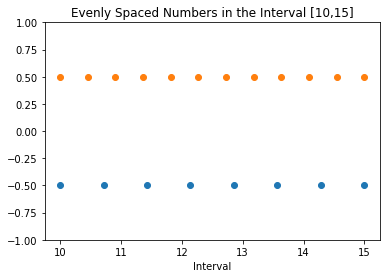
Generowanie równomiernie rozmieszczonych punktów może być pomocne podczas pracy z funkcjami matematycznymi. Dowiemy się o tym w następnej sekcji.
Jak używać NumPy linspace() z funkcjami matematycznymi?
Po wygenerowaniu tablicy równomiernie rozmieszczonych liczb za pomocą np.linspace() , możesz obliczyć wartości funkcji matematycznych w przedziale.
W komórce kodu poniżej najpierw generujesz 50 równomiernie rozmieszczonych punktów w przedziale od 0 do 2π. A następnie utwórz tablicę y za pomocą np.sin() na tablicy x . Pamiętaj, że możesz pominąć parametr num , ponieważ domyślna wartość to 50. Nadal będziemy go używać jawnie.
W następnym kroku możesz wykreślić funkcję sinus w przedziale [0, 2π]. Aby to zrobić, możesz użyć matplotlib, jak w poprzednim przykładzie. W szczególności funkcja plot() w matplotlib.pytplot służy do tworzenia wykresu liniowego.
import numpy as np import matplotlib.pyplot as plt N = 50 a = 0.0 b = 2*np.pi x = np.linspace(a, b, N) y = np.sin(x) plt.plot(x, y, marker = "o") plt.ylim([-1, 1]) plt.title(f'y = sin(x)') plt.xlabel('x ---->') plt.show() 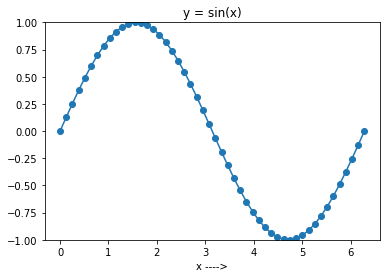
Teraz uruchom powyższy kod, ustawiając N na 10. Otrzymasz wykres, jak pokazano na poniższym rysunku.
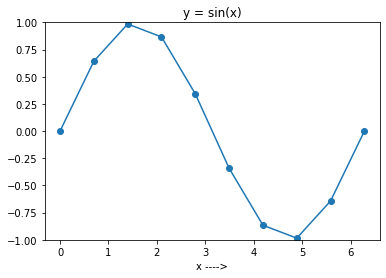
I widać, że wykres nie jest zbyt płynny, ponieważ wybrałeś tylko 10 punktów w przedziale.
Ogólnie rzecz biorąc, im większa liczba rozważanych punktów, tym gładszy będzie wykres funkcji.
Wniosek
Oto podsumowanie tego, czego się nauczyliśmy.
- np.linspace(start, stop, num) zwraca tablicę liczb num równomiernie rozmieszczonych w przedziale [start, stop] .
- Ustaw opcjonalny punkt końcowy parametru na wartość False , aby wykluczyć stop , i ustaw interwał na [start, stop) .
- Ustaw retstep na True opcjonalnie, aby uzyskać rozmiar kroku.
- Generuj tablice o równych odstępach za pomocą np.linspace() , a następnie używaj tablicy z funkcjami matematycznymi.
Mam nadzieję, że teraz rozumiesz, jak działa np.linspace() . Możesz uruchomić powyższe przykłady w notatniku Jupyter. Sprawdź nasz przewodnik po notebooku Jupyter lub innych alternatywach Jupyter, które możesz rozważyć.
Do zobaczenia wkrótce w kolejnym samouczku Pythona. Do tego czasu kontynuuj kodowanie!
