Qu'est-ce que la régression logistique ? Apprenez quand l'utiliser

La vie est pleine de choix binaires difficiles.

Dois-je avoir cette part de pizza ou pas ? Dois-je porter un parapluie ou non?

Alors que certaines décisions peuvent être prises à juste titre en pesant le pour et le contre – par exemple, il vaut mieux ne pas manger une tranche de pizza car elle contient des calories supplémentaires – certaines décisions peuvent ne pas être aussi faciles.

Par exemple, vous ne pouvez jamais être sûr qu'il pleuvra ou non un jour précis. La décision de porter ou non un parapluie est donc difficile à prendre.

Pour faire le bon choix, il faut des capacités prédictives. Cette capacité est très lucrative et a de nombreuses applications dans le monde réel, en particulier dans les ordinateurs. Les ordinateurs aiment les décisions binaires. Après tout, ils parlent en code binaire.

Apprentissage automatique   Les algorithmes, plus précisément l' algorithme de régression logistique , peuvent aider à prédire la probabilité d'événements en examinant des points de données historiques. Par exemple, il peut prédire si un individu gagnera les élections ou s'il pleuvra aujourd'hui.

Si vous vous demandez ce qu'est l'analyse de régression , il s'agit d'un type de technique de modélisation prédictive utilisée pour trouver la relation entre une variable dépendante et une ou plusieurs variables indépendantes.

Un exemple de variables indépendantes est le temps passé à étudier et le temps passé sur Instagram. Dans ce cas, les notes seront la variable dépendante. En effet, à la fois le « temps passé à étudier » et le « temps passé sur Instagram » influenceraient les notes ; l'un positivement et l'autre négativement.

La régression logistique est un algorithme de classification qui prédit un résultat binaire basé sur une série de variables indépendantes. Dans l'exemple ci-dessus, cela signifierait prédire si vous réussirez ou échouerez une classe. Bien sûr, la régression logistique peut également être utilisée pour résoudre des problèmes de régression, mais elle est principalement utilisée pour des problèmes de classification.

Un autre exemple serait de prédire si un étudiant sera accepté dans une université. Pour cela, plusieurs facteurs tels que le score SAT, la moyenne pondérée cumulative de l'élève et le nombre d'activités parascolaires seront pris en compte. À l'aide de données historiques sur les résultats précédents, l'algorithme de régression logistique classera les étudiants en catégories « accepter » ou « rejeter ».

La régression logistique est également appelée régression logistique binomiale ou régression logistique binaire. S'il existe plus de deux classes de la variable de réponse, on parle de régression logistique multinomiale . Sans surprise, la régression logistique a été empruntée aux statistiques et est l'un des algorithmes de classification binaire les plus courants en apprentissage automatique et en science des données.

La régression logistique fonctionne en mesurant la relation entre la variable dépendante (ce que nous voulons prédire) et une ou plusieurs variables indépendantes (les caractéristiques). Pour ce faire, il estime les probabilités à l'aide de sa fonction logistique sous-jacente.

Termes clés de la régression logistique

Comprendre la terminologie est crucial pour déchiffrer correctement les résultats de la régression logistique. Savoir ce que signifient des termes spécifiques vous aidera à apprendre rapidement si vous débutez dans les statistiques ou l'apprentissage automatique.

Qu'est-ce qu'une fonction logistique ?

La régression logistique tire son nom de la fonction utilisée en son cœur, la fonction logistique . Les statisticiens l'ont d'abord utilisé pour décrire les propriétés de la croissance démographique. La fonction sigmoïde et la fonction logit sont quelques variantes de la fonction logistique. La fonction logit est l'inverse de la fonction logistique standard.

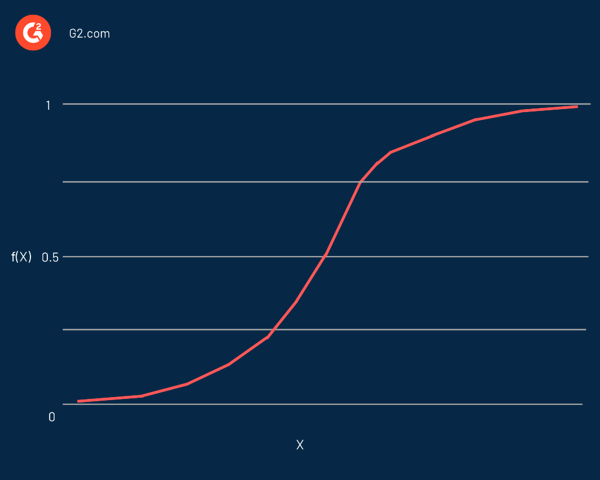
En effet, il s'agit d'une courbe en forme de S capable de prendre n'importe quel nombre réel et de le cartographier en une valeur comprise entre 0 et 1, mais jamais précisément à ces limites. Il est représenté par l'équation :

Dans cette équation :

• f(X) est la sortie de la fonction
• L est la valeur maximale de la courbe
• e est la base des logarithmes naturels
• k est la pente de la courbe
• x est le nombre réel
• x0 est les valeurs x du point médian sigmoïde

Si la valeur prédite est une valeur négative considérable, elle est considérée comme proche de zéro. En revanche, si la valeur prédite est une valeur positive significative, elle est considérée comme proche de un.

La régression logistique est représentée de la même manière que la régression linéaire est définie à l'aide de l'équation d'une ligne droite. Une différence notable par rapport à la régression linéaire est que la sortie sera une valeur binaire (0 ou 1) plutôt qu'une valeur numérique.

Voici un exemple d'équation de régression logistique :

Dans cette équation :

• y est la valeur prédite (ou la sortie)
• b0 est le biais (ou le terme d'interception)
• b1 est le coefficient de l'entrée
• x est la variable prédictive (ou l'entrée)

La variable dépendante suit généralement la   Distribution de Bernoulli. Les valeurs des coefficients sont estimées à l'aide de l'estimation du maximum de vraisemblance (MLE) , de la descente de gradient et de la descente de gradient stochastique .

Comme avec d'autres algorithmes de classification comme le   k-plus proches voisins, a   matrice de confusion   est utilisé pour évaluer la précision de l'algorithme de régression logistique.

Tout comme pour évaluer les performances d'un classificateur, il est tout aussi important de savoir pourquoi le modèle a classé une observation d'une manière particulière. En d'autres termes, nous avons besoin que la décision du classifieur soit interprétable.

Bien que l'interprétabilité ne soit pas facile à définir, son intention première est que les humains sachent pourquoi un algorithme a pris une décision particulière. Dans le cas de la régression logistique, elle peut être combinée avec des tests statistiques comme le   Essai Wald   ou la   test du rapport de vraisemblance   pour l'interprétabilité.

Quand utiliser la régression logistique

La régression logistique est appliquée pour prédire la variable dépendante catégorielle. En d'autres termes, il est utilisé lorsque la prédiction est catégorique, par exemple, oui ou non, vrai ou faux, 0 ou 1. La probabilité prédite ou le résultat de la régression logistique peut être l'un ou l'autre, et il n'y a pas de terrain d'entente.

Dans le cas des variables prédictives, elles peuvent appartenir à l'une des catégories suivantes :

• Données continues : données mesurables à l'infini. Il peut prendre n'importe quelle valeur entre deux nombres. Des exemples sont le poids en livres ou la température en Fahrenheit.
• Données nominales discrètes : données qui correspondent à des catégories nommées. Un exemple rapide est la couleur des cheveux : blond, noir ou brun.
• Données discrètes et ordinales : données qui s'inscrivent dans une certaine forme d'ordre sur une échelle. Un exemple indique à quel point vous êtes satisfait d'un produit ou d'un service sur une échelle de un à cinq.

L'analyse de régression logistique est utile pour prédire la probabilité d'un événement. Il aide à déterminer les probabilités entre deux classes.

Essentiellement, la régression logistique aide à résoudre les problèmes de probabilité et de classification . En d'autres termes, vous ne pouvez vous attendre qu'à des résultats de classification et de probabilité de la régression logistique.

Par exemple, il peut être utilisé pour déterminer la probabilité que quelque chose soit "vrai ou faux" et aussi pour décider entre deux résultats comme "oui ou non".

Un modèle de régression logistique peut également aider à classer les données pour les opérations d'extraction, de transformation et de chargement (ETL). La régression logistique ne doit pas être utilisée si le nombre d'observations est inférieur au nombre d'entités. Sinon, cela peut conduire à un surajustement.

Régression linéaire vs régression logistique

Alors que la régression logistique prédit la variable catégorielle pour une ou plusieurs variables indépendantes,   régression linéaire   prédit la variable continue. En d'autres termes, la régression logistique fournit une sortie constante, tandis que la régression linéaire offre une sortie continue.

Puisque le résultat est continu en régression linéaire, il existe une infinité de valeurs possibles pour le résultat. Mais pour la régression logistique, le nombre de valeurs de résultats possibles est limité.

Dans la régression linéaire, les variables dépendantes et indépendantes doivent être liées de manière linéaire. Dans le cas de la régression logistique, les variables indépendantes doivent être liées linéairement à la   cotes du journal   (log (p/(1-p)).

Alors que la régression linéaire est estimée à l'aide de la méthode des moindres carrés ordinaires, la régression logistique est estimée à l'aide de l'approche d'estimation du maximum de vraisemblance.

La régression logistique et linéaire sont   apprentissage automatique supervisé   algorithmes et les deux principaux types d'analyse de régression. Alors que la régression logistique est utilisée pour résoudre les problèmes de classification, la régression linéaire est principalement utilisée pour les problèmes de régression.

Pour reprendre l'exemple du temps passé à étudier, la régression linéaire et la régression logistique peuvent prédire différentes choses. La régression logistique peut aider à prédire si l'étudiant a réussi ou non un examen. En revanche, la régression linéaire peut prédire le score de l'élève.

Hypothèses de régression logistique

Lors de l'utilisation de la régression logistique, nous faisons quelques hypothèses. Les hypothèses font partie intégrante de l'utilisation correcte de la régression logistique pour faire des prédictions et résoudre des problèmes de classification.

Types de régression logistique

La régression logistique peut être divisée en différents types en fonction du nombre de résultats ou de catégories de la variable dépendante.

Lorsque nous pensons à la régression logistique, nous pensons très probablement à la régression logistique binaire. Dans la plupart des parties de cet article, lorsque nous faisions référence à la régression logistique, nous faisions référence à la régression logistique binaire.

Voici les trois principaux types de régression logistique.

Régression logistique binaire

La régression logistique binaire est une méthode statistique utilisée pour prédire la relation entre une variable dépendante et une variable indépendante. Dans cette méthode, la variable dépendante est une variable binaire, c'est-à-dire qu'elle ne peut prendre que deux valeurs (oui ou non, vrai ou faux, succès ou échec, 0 ou 1).

Un exemple simple de régression logistique binaire consiste à déterminer si un e-mail est un spam ou non.

Régression logistique multinomiale

La régression logistique multinomiale est une extension de la régression logistique binaire. Il permet plus de deux catégories de résultat ou de variable dépendante.

C'est similaire à la régression logistique binaire mais peut avoir plus de deux résultats possibles. Cela signifie que la variable de résultat peut avoir au moins trois types non ordonnés possibles - des types n'ayant aucune signification quantitative. Par exemple, la variable dépendante peut représenter "Type A", "Type B" ou "Type C".

Semblable à la régression logistique binaire, la régression logistique multinomiale utilise également l'estimation du maximum de vraisemblance pour déterminer la probabilité.

Par exemple, la régression logistique multinomiale peut être utilisée pour étudier la relation entre l'éducation et les choix professionnels. Ici, les choix professionnels seront la variable dépendante qui se compose de catégories de différentes professions.

Régression logistique ordinale

La régression logistique ordinale , également appelée régression ordinale, est une autre extension de la régression logistique binaire. Il est utilisé pour prédire la variable dépendante avec trois types ordonnés possibles ou plus - types ayant une signification quantitative. Par exemple, la variable dépendante peut représenter « Fortement en désaccord », « En désaccord », « D'accord » ou « Fortement d'accord ».

Il peut être utilisé pour déterminer le rendement au travail (médiocre, moyen ou excellent) et la satisfaction au travail (insatisfait, satisfait ou très satisfait).

Avantages et inconvénients de la régression logistique

Bon nombre des avantages et des inconvénients du modèle de régression logistique s'appliquent au modèle de régression linéaire. L'un des avantages les plus importants du modèle de régression logistique est qu'il ne se contente pas de classer mais donne également des probabilités.

Cependant, la régression logistique présente de nombreux inconvénients. S'il existe une fonctionnalité qui séparerait parfaitement deux classes, le modèle ne peut plus être formé. C'est ce qu'on appelle la séparation complète .

Cela se produit principalement parce que le poids de cette fonctionnalité ne convergerait pas car le poids optimal serait infini. Cependant, dans la plupart des cas, une séparation complète peut être résolue en définissant une distribution de probabilité a priori des poids ou en introduisant une pénalisation des poids.

Quand la vie vous offre des options, pensez à la régression logistique

Beaucoup pourraient dire que les humains ne vivent pas dans un monde binaire, contrairement aux ordinateurs. Bien sûr, si on vous donne une tranche de pizza et un hamburger, vous pouvez manger les deux sans avoir à en choisir un seul. Mais si vous y regardez de plus près, une décision binaire est gravée sur (littéralement) tout. Vous pouvez choisir de manger ou de ne pas manger une pizza ; il n'y a pas de juste milieu.

L'évaluation des performances d'un modèle prédictif peut être délicate si la quantité de données est limitée. Pour cela, vous pouvez utiliser une technique appelée validation croisée, qui consiste à partitionner les données disponibles en un ensemble d'apprentissage et un ensemble de test.