什么是逻辑回归？ 了解何时使用它

生活充满了艰难的二元选择。

我应该吃那片披萨吗？ 我应该带伞还是不带伞？

虽然有些决定可以通过权衡利弊来做出正确的决定——例如，最好不要吃一片比萨饼，因为它含有额外的卡路里——但有些决定可能并不那么容易。

例如，您永远无法完全确定某一天是否会下雨。 所以要不要带雨伞是一个艰难的决定。

为了做出正确的选择，需要预测能力。 这种能力非常有利可图，并且在现实世界中有许多应用，尤其是在计算机中。 计算机喜欢二元决策。 毕竟，他们说的是二进制代码。

机器学习  算法，更准确地说是逻辑回归算法，可以通过查看历史数据点来帮助预测事件的可能性。 For example, it can predict whether an individual will win the election or whether it'll rain today.

如果您想知道什么是回归分析，它是一种预测建模技术，用于查找因变量与一个或多个自变量之间的关系。

自变量的一个例子是花在学习上的时间和花在 Instagram 上的时间。 在这种情况下，成绩将是因变量。 这是因为“学习时间”和“在 Instagram 上花费的时间”都会影响成绩； 一个是积极的，另一个是消极的。

逻辑回归是一种基于一系列自变量预测二元结果的分类算法。 在上面的例子中，这意味着预测你是否会通过或失败。 当然，逻辑回归也可以用来解决回归问题，但主要用于分类问题。

另一个例子是预测学生是否会被大学录取。 为此，将考虑SAT分数、学生的平均成绩和课外活动的数量等多种因素。 使用有关先前结果的历史数据，逻辑回归算法将学生分为“接受”或“拒绝”类别。

逻辑回归也称为二项逻辑回归或二元逻辑回归。 如果响应变量的类别超过两类，则称为多项逻辑回归。 毫不奇怪，逻辑回归是从统计学中借用的，是机器学习和数据科学中最常见的二元分类算法之一。

逻辑回归通过测量因变量（我们想要预测的）和一个或多个自变量（特征）之间的关系来工作。 它通过在其基础逻辑函数的帮助下估计概率来做到这一点。

逻辑回归中的关键术语

理解术语对于正确解读逻辑回归的结果至关重要。 如果您不熟悉统计或机器学习，了解特定术语的含义将有助于您快速学习。

什么是逻辑函数？

逻辑回归以其核心使用的函数命名，逻辑函数。 统计学家最初用它来描述人口增长的特性。 Sigmoid 函数和logit 函数是逻辑函数的一些变体。 Logit 函数是标准逻辑函数的逆函数。

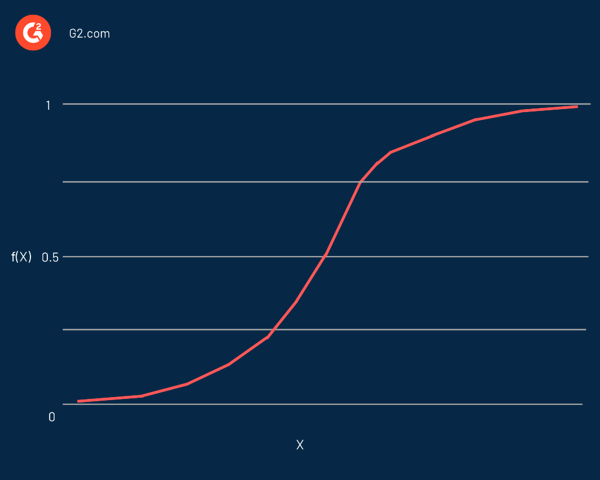
实际上，它是一条 S 形曲线，能够取任何实数并将其映射为 0 到 1 之间的值，但绝不会精确到这些限制。 它由等式表示：

在这个等式中：

• f(X)是函数的输出
• L是曲线的最大值
• e是自然对数的底
• k是曲线的陡度
• x是实数
• x0是 sigmoid 中点的 x 值

如果预测值是相当大的负值，则认为它接近于零。 另一方面，如果预测值是一个显着的正值，则认为它接近一个。

逻辑回归的表示方式类似于使用直线方程定义线性回归的方式。 与线性回归的一个显着区别是输出将是二进制值（0 或 1）而不是数值。

这是逻辑回归方程的示例：

在这个等式中：

• y是预测值（或输出）
• b0是偏差（或截距项）
• b1是输入的系数
• x是预测变量（或输入）

因变量通常遵循  伯努利分布。 使用最大似然估计 (MLE) 、梯度下降和随机梯度下降来估计系数的值。

与其他分类算法一样，如  k-最近邻，a   混淆矩阵  用于评估逻辑回归算法的准确性。

就像评估分类器的性能一样，了解模型为什么以特定方式对观察进行分类同样重要。 换句话说，我们需要分类器的决定是可解释的。

尽管可解释性不容易定义，但其主要目的是人类应该知道算法为何做出特定决定。 在逻辑回归的情况下，它可以与统计测试相结合，如  沃尔德测试  或者  似然比检验  为了可解释性。

何时使用逻辑回归

逻辑回归用于预测分类因变量。 换句话说，它用于预测是分类的，例如是或否，真或假，0或1。逻辑回归的预测概率或输出可以是其中之一，没有中间立场。

在预测变量的情况下，它们可以是以下任何类别的一部分：

• 连续数据：可以在无限范围内测量的数据。 它可以取两个数字之间的任何值。 例如，以磅为单位的重量或以华氏度为单位的温度。
• 离散的名义数据：适合命名类别的数据。 一个简单的例子是头发颜色：金色、黑色或棕色。
• 离散的有序数据：符合某种规模顺序的数据。 一个例子是告诉你对产品或服务的满意程度，从一到五。

逻辑回归分析对于预测事件的可能性很有价值。 它有助于确定任何两个类别之间的概率。

从本质上讲，逻辑回归有助于解决概率和分类问题。 换句话说，您只能期望逻辑回归的分类和概率结果。

例如，它可用于确定某事为“真或假”的概率，也可用于在“是或否”等两种结果之间做出决定。

逻辑回归模型还可以帮助对提取、转换和加载 (ETL) 操作的数据进行分类。 如果观察数少于特征数，则不应使用逻辑回归。 否则，可能会导致过拟合。

线性回归与逻辑回归

虽然逻辑回归预测一个或多个自变量的分类变量，   线性回归  预测连续变量。 换句话说，逻辑回归提供恒定输出，而线性回归提供连续输出。

由于结果在线性回归中是连续的，因此结果有无限可能的值。 但是对于逻辑回归，可能的结果值的数量是有限的。

在线性回归中，因变量和自变量应该是线性相关的。 在逻辑回归的情况下，自变量应与  对数赔率  (log (p/(1-p))。

虽然使用普通最小二乘法估计线性回归，但使用最大似然估计方法估计逻辑回归。

逻辑回归和线性回归都是  监督机器学习  算法和回归分析的两种主要类型。 虽然逻辑回归用于解决分类问题，但线性回归主要用于回归问题。

回到学习时间的例子，线性回归和逻辑回归可以预测不同的事情。 逻辑回归可以帮助预测学生是否通过了考试。 相比之下，线性回归可以预测学生的分数。

逻辑回归假设

在使用逻辑回归时，我们做了一些假设。 假设对于正确使用逻辑回归进行预测和解决分类问题是不可或缺的。

逻辑回归的类型

逻辑回归可以根据因变量的结果数量或类别分为不同的类型。

当我们想到逻辑回归时，我们很可能会想到二元逻辑回归。 在本文的大部分内容中，当我们提到逻辑回归时，我们指的是二元逻辑回归。

以下是逻辑回归的三种主要类型。

二元逻辑回归

二元逻辑回归是一种统计方法，用于预测因变量和自变量之间的关系。 在这种方法中，因变量是一个二元变量，这意味着它只能取两个值（是或否、真或假、成功或失败、0 或 1）。

二元逻辑回归的一个简单示例是确定电子邮件是否为垃圾邮件。

多项逻辑回归

多项逻辑回归是二元逻辑回归的扩展。 它允许超过两个类别的结果或因变量。

它类似于二元逻辑回归，但可以有两个以上的可能结果。 这意味着结果变量可以具有三个或更多可能的无序类型——没有数量意义的类型。 例如，因变量可以表示“A 型”、“B 型”或“C 型”。

与二元逻辑回归类似，多项逻辑回归也使用最大似然估计来确定概率。

例如，多项逻辑回归可以用来研究一个人的教育和职业选择之间的关系。 在这里，职业选择将是由不同职业类别组成的因变量。

序数逻辑回归

序数逻辑回归，也称为序数回归，是二元逻辑回归的另一种扩展。 它用于预测具有三个或更多可能的有序类型的因变量——具有定量意义的类型。 例如，因变量可以表示“非常不同意”、“不同意”、“同意”或“非常同意”。

它可用于确定工作绩效（差、平均或优秀）和工作满意度（不满意、满意或非常满意）。

逻辑回归的优缺点

逻辑回归模型的许多优点和缺点都适用于线性回归模型。 逻辑回归模型最显着的优势之一是它不仅可以分类，还可以给出概率。

然而，逻辑回归有许多缺点。 如果有一个特征可以完美地分离两个类，那么这个模型就不能再训练了。 这称为完全分离。

这主要是因为该特征的权重不会收敛，因为最佳权重将是无限的。 然而，在大多数情况下，完全分离可以通过定义权重的先验概率分布或引入权重的惩罚来解决。

当生活给你选择时，想想逻辑回归

许多人可能会争辩说，与计算机不同，人类并不生活在二进制世界中。 当然，如果给你一片披萨和一个汉堡包，你可以两口都吃，而不必只选择一个。 但是，如果您仔细观察它，就会发现（字面上）一切都刻有二元决定。 你可以选择吃或不吃披萨； 没有中间立场。

如果数据量有限，评估预测模型的性能可能会很棘手。 为此，您可以使用一种称为交叉验证的技术，该技术涉及将可用数据划分为训练集和测试集。